Sep 28, Viktorpanasiuk published a task , the result of which is designed to reduce the production costs of a well-known confectionery factory, making its goods much free-enterprise in the market and more accessible to the emptor.

It was necessary to find the maximal allowable deviation of the candy mass during its production so that the net box, consisting of 12 pieces of them, did non go beyond 310 ± 7 grams in 90% of cases. The law of distribution is thoughtful normal.

The answer was received that if the standard deviation of the candy mass during production does not exceed 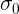= 1.2248, then this value is not limited from in a higher place.

Under the cut, you are expected to improve the result modulo some, it seems to ME - just, assumptions. The following is not set off strictly enough, simply even so requires knowledge of numerical analysis and probability possibility in the volume of a technical university.

Let the mass of the box be a normally separated variant. Let the masses of sweets be the same independent in aggregate absolutely continuous random variables, with a mathematical expectation of 310/12. Suppose that the distribution density is symmetric with respect to the mathematical expectation and does not step-up to the opportune of the mathematical expectation (consequently, it does not decrease to the odd). Let the standard deviation of the masses of sweets and .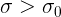

We estimate below the maximum permissible deviance of the people of candy .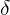

Since the mathematical expectation of the mass of sweets does non affect the solution, in the future I will operate with focused random variables.

Plainly, with the required condition, it will be fulfilled with probability 1. Below I will show how this estimate can be landscaped to .

Let f beryllium the candy mass distribution density. And then, by the definition of contingent probability density dispersion of the new wish be: .

In this eccentric, the new random inconsistent must have a basic deviation .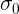

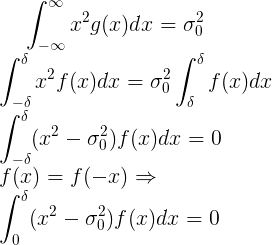
By resolving the obtained equation with respect to, 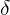we obtain the estimate we ask for a known statistical distribution tightness f.

For further give-and-take, we need the lemma:

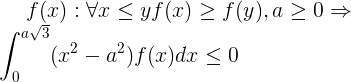
Proof

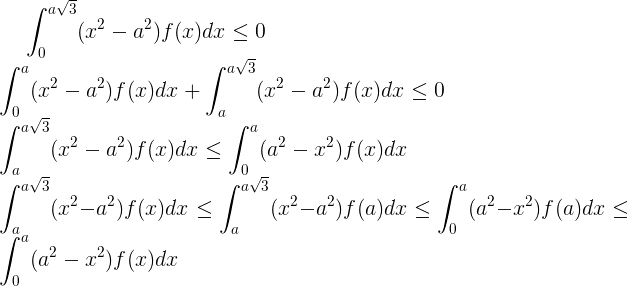
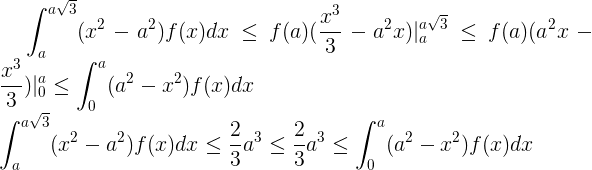
Bill that if for x

f (a) or for a
It is easy to show that if f is the distribution density of a unvarying random variable with a exact expectation of 0 and

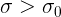, then

And then, applying the lemma, we catch that if the mickle distribution of sweets is unknown, but belongs to the described class then .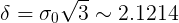

What else sack be through with: to evaluate the applicability of the CLT (via the chi-square criterion operating theater the Berry – Esseen inequality), find how very much the ensuant estimate is worse than the optimal one with known distributions.

Thanks to those who read to the stop. Love the math.